Project Info

Name:Time Table Scheduling Started:2024-10-26 Finished:2025-02-28 Source Code

Table of Contents

Time Table Scheduling Bruteforce vs Genetic Algorithm API Endpoints Documentation What I learned Example Data

Time Table Scheduling

Overview

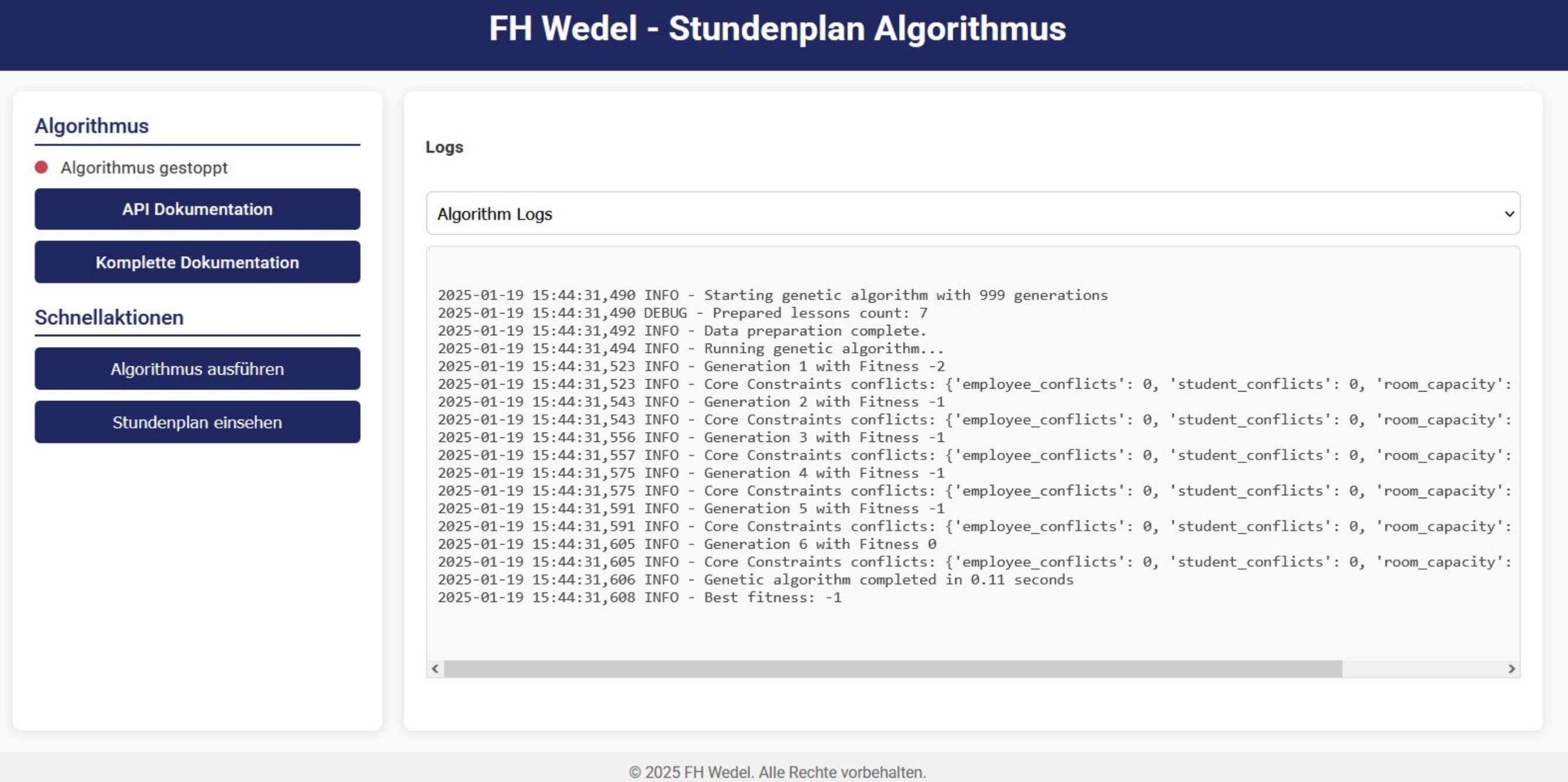
Time Table Scheduling is a Python-based application for generating optimized timetables using the PyGad Genetic Algorithm Library. The project is packaged as a Docker container for easy deployment and provides a RESTful API for interaction.

A genetic-algorithm approach has been chosen because scheduling a TimeTable is an NP-Hard problem, meaning there exists no efficient algorithm to solve it.

Technologies Used

Python
PyGad Genetic Algorithm Library
Docker
Swagger API Documentation
Basic Frontend for log insights and quick actions

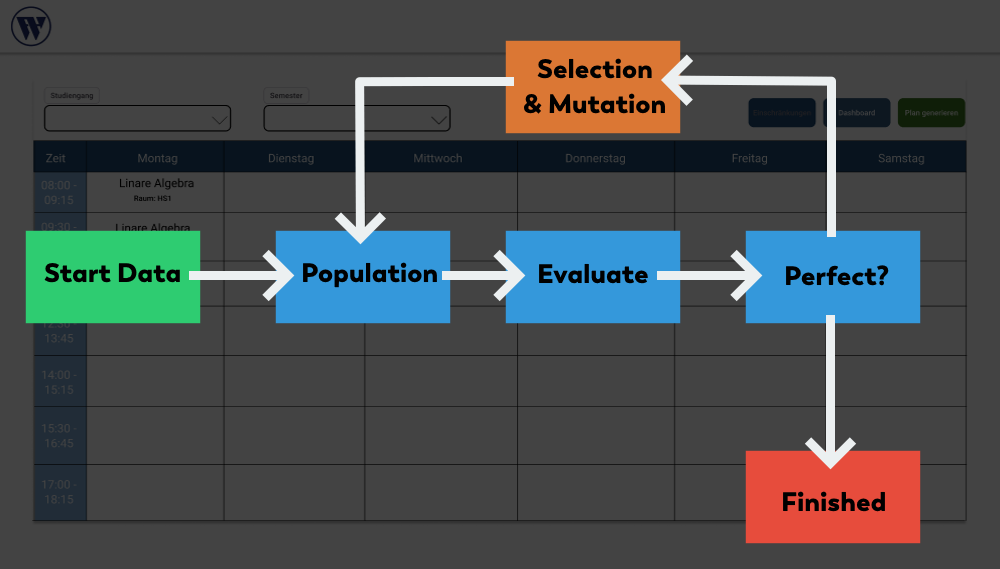
Genetic Algorithm

The genetic algorithm starts with an initial population of randomly generated timetables. Each timetable is evaluated against the input constraints, mimicking natural selection. The best-performing timetables are selected to create a new population with small modifications (mutations). This process repeats until an optimal timetable is found that satisfies all constraints.

genetic algorithm

Limitations of the Genetic Algorithm

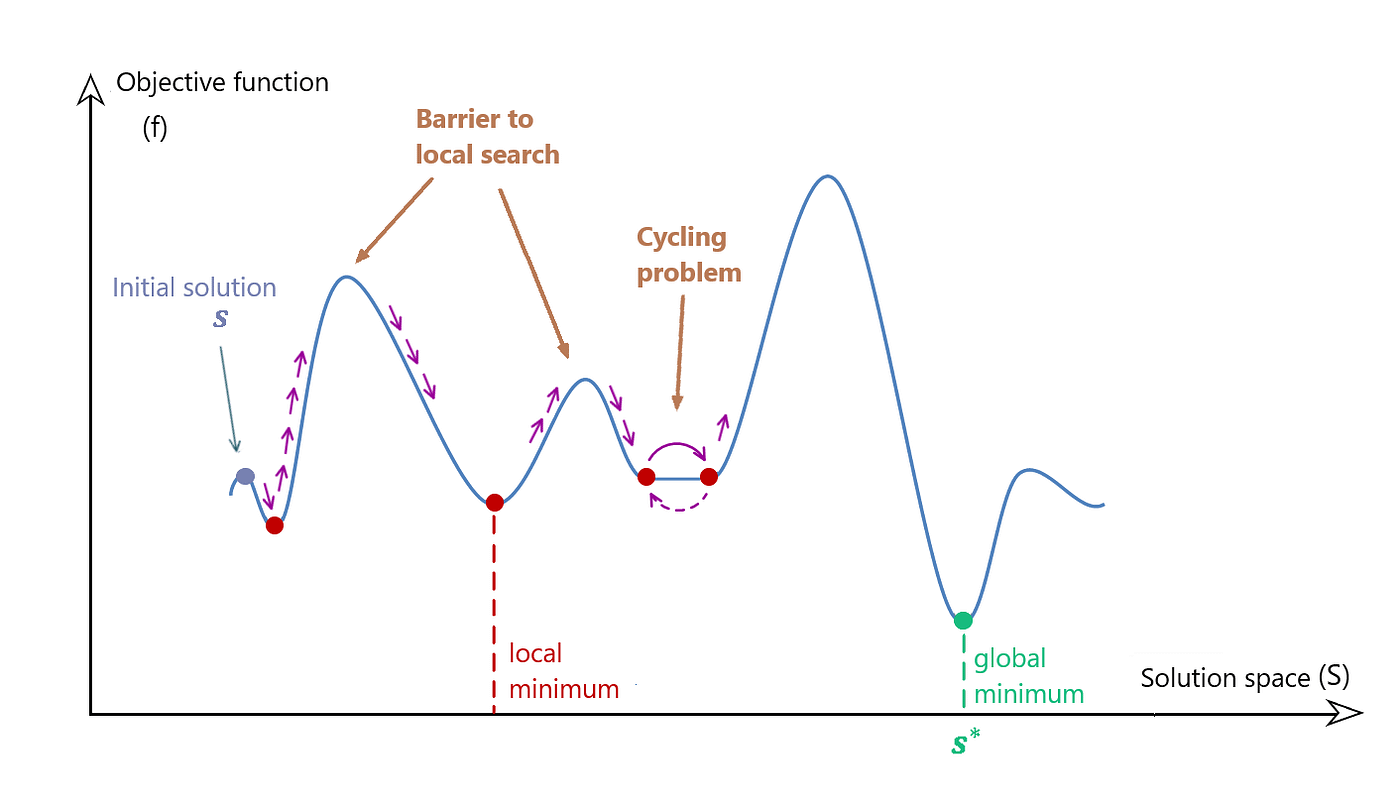
To describe the picture first, on the y-axis higher values represent worse results and lower values represent better results, the global minimum is the best timetable that can be created.

Genetic algorithms tend to rest at local minimums, because to find the next better local or global minimum, they must first mutate to a worse result. This is because the mutations happen randomly. If the global minimum (optimal solution) is very narrow compared to the overall solution space the genetic algorithm will have big trouble finding it, and it would be a statistical anomaly for the random mutations to result in the optimal result, depending on the overall complexity it can be considered to happen never because it is so unlikely.

Bruteforce vs Genetic Algorithm

Consider a search space defined by:

t: Number of timeslots
e: Number of events

The total number of possible solutions is:
N = t^e

Assume there is exactly one valid solution s*.

1. Brute-Force Approach

The brute-force method systematically enumerates every possibility without duplication.

Probability of Success per Trial

Since there is one correct solution among N possibilities, if evaluated in a random order the probability of finding s* in any unique trial is:
P_BF = 1 / t^e

Expected Number of Trials

Average Case:
If the correct solution is equally likely to appear in any position, the expected number of unique evaluations is:
E_BF = (N + 1) / 2 ≈ t^e / 2
Worst Case:
In the worst-case scenario, the algorithm checks all possibilities:
E_BF, worst = t^e

Because brute-force never repeats a check, it is optimal in terms of covering the search space without redundancy.

2. Genetic Algorithm (GA) Approach

In the worst-case scenario, the GA behaves like a random search with replacement, meaning the same candidate solution might be generated multiple times.

Probability of Success per Evaluation

Each candidate solution generated by mutation (or uninformative crossover) is an independent random sample from the t^e possibilities:
P_GA = 1 / t^e

Expected Number of Evaluations

Let X be the number of evaluations required to find s*. Since each trial is independent, X follows a geometric distribution with success probability p = 1 / t^e. The expectation for a geometric distribution is:
E[X] = 1 / p = t^e
Thus, on average, the GA requires t^e evaluations.

Impact of Duplicate Evaluations

Unlike the brute-force method, the GA can sample the same solution more than once. These duplicates do not bring the search any closer to finding the unique correct solution. Therefore, while both approaches have a per-trial success probability of 1 / t^e, the systematic nature of brute-force (avoiding repeats) makes it more efficient in terms of unique evaluations.

3. Conclusion

Brute-Force:
E_BF ≤ t^e (systematic, non-duplicate evaluation)
Genetic Algorithm:
E_GA ≈ t^e (random sampling with possible duplicates)

Thus, in the worst-case scenario:
E_GA ≥ E_BF

The absence of duplicate checks in brute-force means it is, in expectation, more efficient than a GA that behaves like a random search in a search space with exactly one valid solution.

Application of Bruteforce

My university is scheduling the TimeTable for 5 days with 7 timeslots each, and it has roughly 236 individual events that have to be scheduled. This results in a total solution space of N = (5 * 7)^236 which is a number that looks like this:

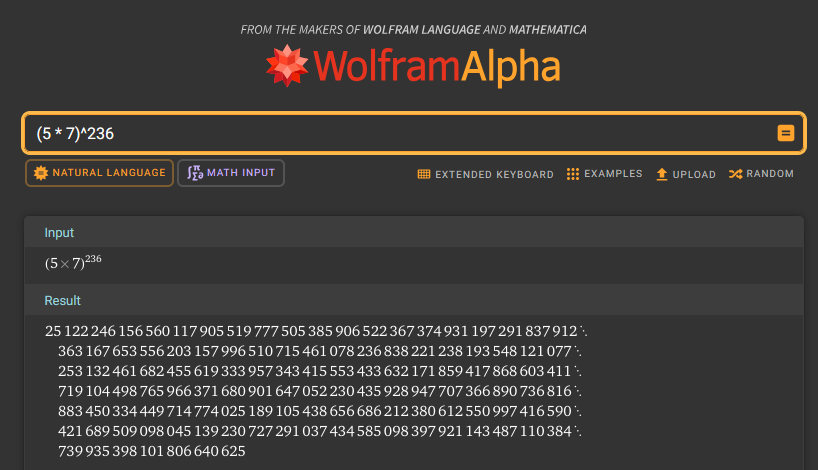
As one can imagine, even with the best computing power these days, bruteforcing this problem would not finish in our lifetimes. So even if bruteforce is mathmatically better, a genetic algorithm is still preferred, as it might not return the optimal result, but still a very good one.

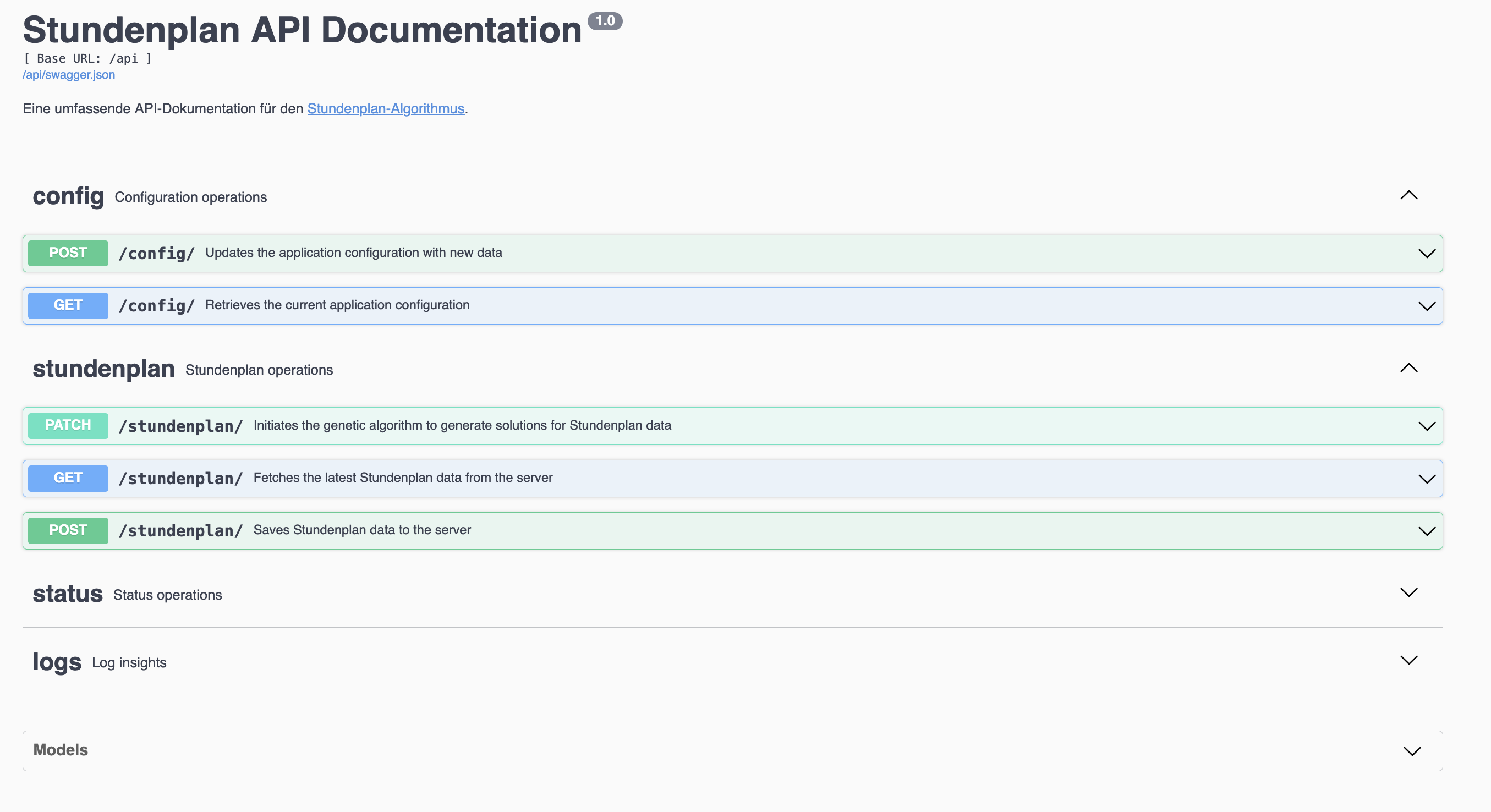
API Endpoints

Timetable Management

POST /api/stundenplan
Upload a dataset that will be used by the algorithm to generate a timetable.
PUT /api/stundenplan
Start the genetic algorithm to generate a timetable. This may take a long time due to the problem being NP-complete. (Was previously PATCH, PUT had to be used to work with the Spring Frontend)
GET /api/stundenplan
Retrieve the generated timetable.

Configuration

GET /api/config
Fetch the current system configuration.
POST /api/config
Modify configuration settings, such as the maximum number of generations.

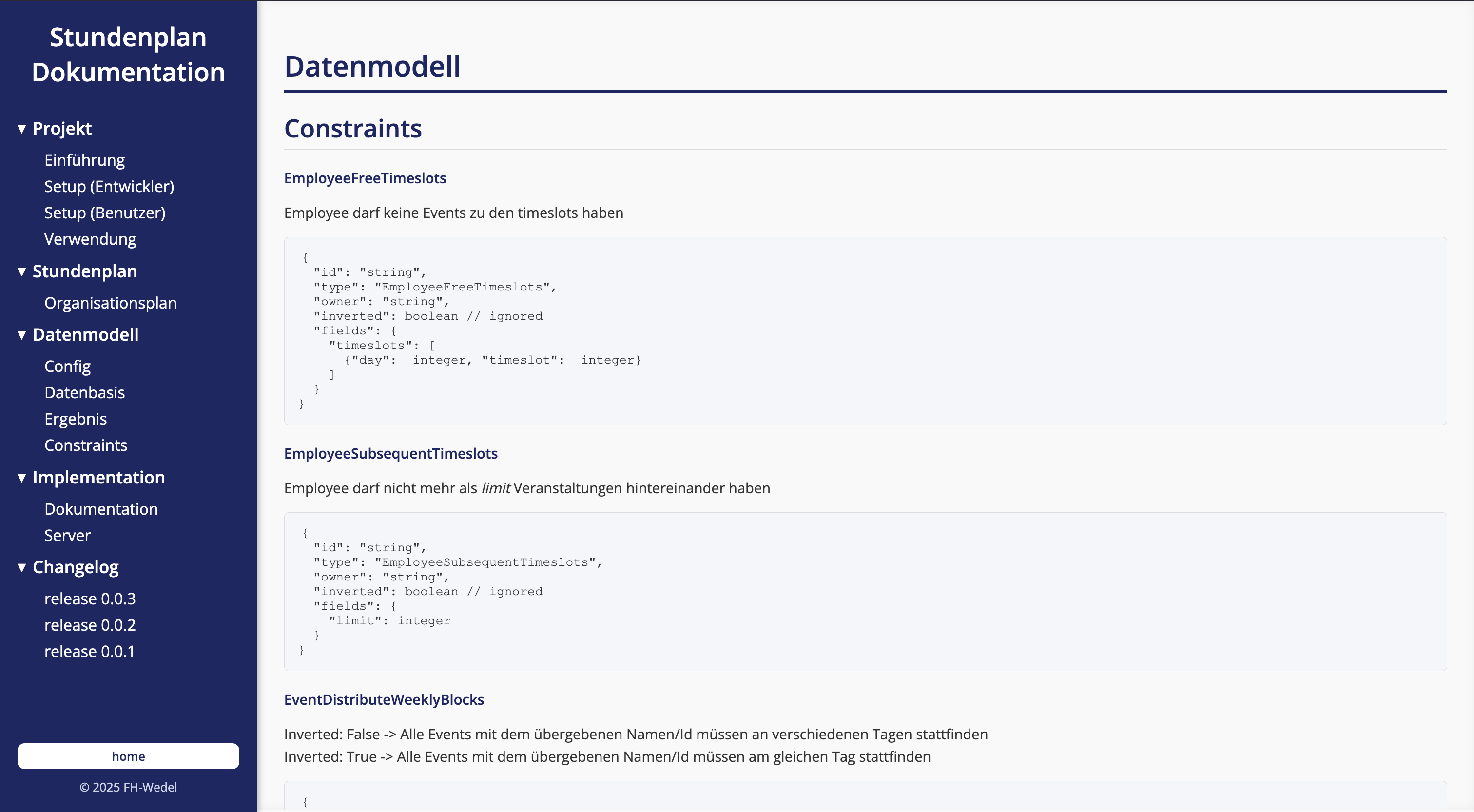
Constraints

The scheduling algorithm considers multiple constraints, including:

Core Constraints – These fundamental rules ensure that the schedule remains valid at all times. They include:
- No lecturer or participant is assigned to multiple events at the same time.
- No room is allocated to more than one event simultaneously.
- Events must be scheduled within valid time slots.
EmployeeSubsequentTimeslots – Limits the number of consecutive scheduled events for an employee.
EventDistributeWeeklyBlocks – Ensures events with multiple blocks are distributed across different days.
EmployeeFreeTimeslots – Prevents scheduling events for an employee at specific times.

Deployment

The project is implemented as a Docker container, making it easily deployable in various environments.

Implementation Details

This project has implemented unit tests to verify constraint fulfillment. A big factor was making it robust, so all input data is thoroughly being verified to contain only valid and all necessary data with detailed error messages.

Documentation

For the entire software project a Documentation is available. The algorithm is my part.

API Documentation

Swagger API documentation is available at /api/docs.

General Documentation

A full documentation is self contained in the project at /docs include an architecture decision record and a comprehensive changelog.

What I learned

I learned the value of teamwork in this project, where each member had clearly defined responsibilities. We collaborated by creating and sharing Docker images, ensuring a smooth workflow while maintaining individual accountability. This experience gave me a deeper understanding of effective team coordination and task management.

Example Data

Input Data:

{
  "timeslots": [
    {
      "day": 1,
      "timeslot": 1
    },
    {
      "day": 1,
      "timeslot": 2
    },
    ...
  ],
  "rooms": [
    {
      "name": "SR01",
      "capacity": 20,
      "room_type": "Seminarraum"
    },
    {
      "name": "HS01",
      "capacity": 20,
      "room_type": "Hörsaal"
    }
  ],
  "events": [
    {
      "name": "Statistik",
      "employees": [
        "BOE"
      ],
      "participants": [
        "B_INF"
      ],
      "size": 20,
      "weekly_blocks": 4,
      "room_type": "Hörsaal"
    }
  ],
  "constraints": {
    "hard": [
      {
        "type": "EventDistributeWeeklyBlocks",
        "owner": "BOE",
        "inverted": false,
        "fields": {
          "event": "Statistik"
        }
      }
    ],
    "soft": []
  }
}

Example Time Table Result

{
  "data": {
    "timetable": [
      {
        "day": 1,
        "timeslot": 1,
        "event": "Statistik",
        "room": "HS01",
        "participants": [
          "B_INF"
        ]
      },
      {
        "day": 2,
        "timeslot": 7,
        "event": "Statistik",
        "room": "HS01",
        "participants": [
          "B_INF"
        ]
      },
      {
        "day": 4,
        "timeslot": 3,
        "event": "Statistik",
        "room": "HS01",
        "participants": [
          "B_INF"
        ]
      },
      {
        "day": 3,
        "timeslot": 6,
        "event": "Statistik",
        "room": "HS01",
        "participants": [
          "B_INF"
        ]
      }
    ],
    "metadata": {
      "fitness": 0
    },
    "constraints": {
      "core": {
        "fitness": 0,
        "unsatisfied": {
          "employee_conflicts": 0,
          "student_conflicts": 0,
          "room_capacity": 0,
          "room_type": 0
        },
        "satisfied": {
          "employee_conflicts": 4,
          "student_conflicts": 4,
          "room_capacity": 4,
          "room_type": 4
        }
      },
      "hard": {
        "fitness": 0,
        "unsatisfied": [],
        "satisfied": [
          {
            "id": null,
            "type": "EventDistributeWeeklyBlocks",
            "owner": "BOE",
            "inverted": false,
            "fields": {
              "event": "Statistik"
            }
          }
        ]
      },
      "soft": {
        "fitness": 0,
        "unsatisfied": [],
        "satisfied": []
      }
    }
  },
  "timestamp": "2025-02-25T13:37:01.522647",
  "status": "success"
}

Written: 2025-03-08